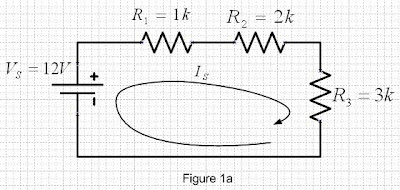
1. Voltage and Curret in Series
Example :
As we can see above, all component is in series. And we know that, if the component in series so :
1. each component ( R1,R2, and R3) will has the same Current = Is.
2. each component will has the different voltage, and it's depend on its value of R.
Because of in series, so we can replace all R1, R2, and R3 become Rs. Rs = R1 + R2 + R3.
Rs = 1k + 2k +3k
= 6k
To analize it, first of all, we make the simplest circuit as below.
By implementing Ohm's law. V = I x R ---> I = V / R
Is = Vs / Rs
= 12V / 6k
= 2mA
Because current in each load (R1,R2,R3) is the same current, so we can calculate voltage in each load.
Voltage for R1 ---> V1 = Is. R1 = 2mA. 1k = 2V
Voltage for R2 ---> V2 = Is. R2 = 2mA. 2k = 4V
Voltage for R3 ---> V3 = Is. R3 = 2mA. 3k = 6V
By using Kirchoff's Law for Voltage.Total voltage in closed loop circuit must be zero 0.
-Vs + V1 + V2+V3 = 0
-12V + 2V + 4V + 6V =0 --> tried-and-true.
2. Voltage and current in parallel
Example :
As we can see above, R2 and R3 is in parallel, but R2 and R3 is in series to R1. In this case Current I1 will be divided into R2 and R3. So I1=I2 + I3.
In order to get value of I1, I2, and I3. First off all, we make the circuit simpler, as below.
Rp is a parallel form of R2 dan R3. Rp = R2 // R3
1/Rp = 1/R2 + 1/R3 or Rp = (R2 . R3) / (R2+R3) = 1.2k
If we look circuit above, R1 is in series to Rp become Rs. Rs = R1 + Rp. Rs = 1k + 1.2k = 2.2k
And finally we can make the simplest circuit as below.
From figure 2c above, we can measure I1, I1=Vs / Rs = 12V / 2.2 k = 5.45mA
then, we can calculate voltage for Rp.
Voltage at Rp is Voltage at B Node = VB. VB=I1.Rp
VB = 5.45mA . 1.2k
= 6.54 V
Because Rp is R2 parallel to R3. So that, Voltage at R2 = Voltage at R3.
VB = VC = 6.54 V
I2 = VB / R2
= 6.54V / 2k
= 3.27 mA
By using Current Kirchoff's law ( Kirchoff I ),
I1 = I2 + I3 -----> I3 = I1 - I2
I3 = 5.45 mA - 3.27 mA
I3 = 2.18 mA
VAB =..?, ---> means voltage at A node with refference B node
VAB = VA - VB
= 12 V - 6.54 V
= 5.46 V






No comments:
Post a Comment